Analysing Fairness in Machine Learning
Doing an exploratory fairness analysis and measuring fairness using equal opportunity, equalized odds and disparate impact

It is no longer enough to build models that make accurate predictions. We also need to make sure that those predictions are fair.
Doing so will reduce the harm of biased predictions. As a result, you will go a long way in building trust in your AI systems. To correct bias we need to start by analysing fairness in data and models.
Measuring fairness is straightforward.
Understanding why a model is unfair is more complicated.
This is why we will:
- First do an exploratory fairness analysis – to identify potential sources of bias before you start modelling.
- We will then move on to measuring fairness – by applying different definitions of fairness.
You can see a summary of the approaches we will cover below.

We will discuss the theory behind these approaches. We will also be applying them using Python. We will discuss key pieces of code and you can find the full project on GitHub.
You can also watch these videos as an introduction to the topics:
Dataset
We will be building a model using the Adult Data Set. You can see a snapshot of this in Table 1. After a bit of feature engineering, we will be using the first 6 columns as model features. The next 2, race and sex, are sensitive attributes. We will be analysing bias towards groups based on these. The last is our target variable. We will try to predict if a person's income is above or below $50K.

Before we load this dataset, we need to import some Python packages. We do this with the code below. We use NumPy and Pandas for data manipulation (lines 1–2). Matplotlib is used for some data visualisations (line 3). We will be using xgboost to build our model (line 5). We also import some functions from scikit-learn to assess our model (lines 7–9). Make sure you have these installed.
We import our dataset below (line 7). We also drop any rows that have a missing value (line 8). Note there are some additional columns loaded here. See the column names (lines 1–4). In this analysis, we will only consider those we mentioned in Table 1.
Exploratory analysis for algorithm fairness
Assessing fairness does not start when you have your final model. It should also be a part of your exploratory analysis. In general, we do this to build some intuition around our dataset. So, when it comes to modelling, you have a good idea of what results to expect. Specifically, for fairness, you want to understand what aspects of your data may lead to an unfair model.
Your model can become unfair due to different reasons for unfairness. In our exploratory analysis, we will focus on 3 key sources that relate to data. These are historical bias, proxy variables and unbalanced datasets. We want to understand the extent to which these are present in our data. Understanding the reasons will help us choose the best approach for addressing unfairness.
Unbalanced datasets
We will start by seeing if our dataset is unbalanced. Specifically, we mean unbalanced in terms of the sensitive attributes. Looking at Figure 1, we have the breakdown of the population by race and sex. You can see that we do have an unbalanced dataset. The first chart shows that 86% of our population is white. Similarly, 68% of the population is male.

You can see how we created the pie chart for the race attribute below. We start by creating a count of the population by race (line 2). We define labels using the index (line 3). These are the names of the different race groups we see in Figure 1. We then plot the counts using the pie function from matplotlib (line 6). We also create a legend using the labels (line 7). The code for the sex attribute pie chart is very similar.
The issue with an unbalanced dataset is that model parameters can become skewed towards the majority. For example, the trends could be different for the female and male populations. By trends, we mean relationships between features and the target variable. A model will try to maximise accuracy across the entire population. In doing so it may favour trends in the male population. As a consequence, we can have a lower accuracy on the female population.
Defining protected features
Before we move on, we will need to define our protected features. We do this by creating binary variables using the sensitive attributes. We define the variable so that 1 represents a privileged group and 0 represents an unprivileged group. Typically, the unprivileged group will have faced historical injustice in the past. In other words, it is the group that will most likely face unfair decisions from a biased model.
We define these features using the code below. For race, we define the protected feature so that “White” is the privileged group (line 4). That is the variable has a value of 1 if the person is white and 0 otherwise. For sex, “Male” is the privileged group (line 5). Going forward, we will use these binary variables instead of the original sensitive attributes.
In the above code, we have also defined a target variable (line 8). Where it has a value of 1 if the person earns above $50K and 0 if they earn below $50K. In line 1, we created the df_fair dataset with the original sensitive attributes. We have added the target variable and protected features to this dataset. It will be used as a base for the remaining fairness analysis.
Prevalence
For a target variable, prevalence is the proportion of the positive cases to overall cases. Where a positive case is when the target variable has a value of 1. Our dataset has an overall prevalence of 24.8%. That is roughly 1/4 of the people in our dataset earn above $50K. We can also use prevalence as a fairness metric.
We do this by calculating prevalence for our different privileged (1) and unprivileged (0) groups. You can see these values in Table 2 below. Notice that the prevalence is much higher for the privileged groups. If fact, if you are male you are nearly 3 times as likely to earn above $50K than if you are female.

We can go further by calculating the prevalence at the intersection of the protected features. You can see these values in Table 3. The top left corner gives the prevalence if you are in both privileged groups (i.e sex = 1 & race = 1). Similarly, the bottom right gives the prevalence if you are in neither privileged group (i.e sex = 0 & race = 0). This tells us that white males are over 4 times as likely to earn above $50K than non-white females.

We calculate these values using the code below. You can see that overall prevalence is just the average of the target variable (line 1). Similarly, we can take the average for the different protected feature combinations (lines 3–5).
At this point, you should be asking yourself why we have these large differences in prevalence. The dataset was built using United States census data from 1994. The country has a history of discrimination based on gender and race. Ultimately, the target variable reflects this discrimination. In this sense, prevalence can be used to understand the extent to which historical injustice is embedded in our target variable.
Proxy variables
Another way we can analyse potential sources of bias is by finding proxy variables. These are model features that are highly correlated or associated with our protected features. A model that uses a proxy variable can effectively be using a protected feature to make decisions.
We can find proxy variables in a similar way to how you find important features during feature selection. That is we use some measure of association between the features and target variable. Except now, instead of the target variable, we use the protected features. We will look at two measures of association — mutual information and feature importance.
Before that, we need to do some feature engineering. We start by creating a target variable just as before (line 2). We then create 6 model features. To start, we leave age, education-num and hours-per-week as is (line 5). We create binary features from marital-status and native-country (lines 6–7). Lastly, we create the occupation feature by grouping the original occupations into 5 groups (lines 9–16). In the next section, we will use these same features to build our model.
Mutual information is a measure of non-linear association between two variables. It indicates how much the uncertainty around one variable is reduced by observing another. In Figure 2, you can see the mutual information values between each of the 6 features and protected features. Notice the high value between marital-status and sex. This suggests a possible relationship between these variables. In other words, marital-status could be a proxy variable for sex.

We calculate the mutual information values using the code below. This is done using the mutual_info_classif function. For race, we pass our feature matrix (line 2) and race protected feature (line 3). We also tell the function which of the 6 features are discrete (line 4). The code is similar for sex (line 5).
Another approach we can take is to build a model using the protected features. That is we try to predict the protected feature using the 6 model features. We can then use feature importance scores from this model as our measure of association. You can see the result of this process in Figure 3.

Another result of this process is that we have the model accuracy. These can give us a measure of overall association. The accuracy was 72.7% when predicting race and 78.9% when predicting sex. This difference makes sense if we go back to the mutual information values in Figure 2. You can see the values were generally higher for sex. Ultimately, we could expect proxy variables to be more of a problem for sex than race.
You can see how we calculate the metrics for race below. We start by getting a balanced sample (lines 2–7). This is so we have the same number of privileged and unprivileged in our dataset. We then use this dataset to build a model (lines 10 -11). Notice that we are using the race protected feature as the target variable. We then get the model predictions (line 12), calculate accuracy (line 15) and get the feature importance scores (line 18).
So, we have seen that the dataset is unbalanced and prevalence is higher for privileged groups. We have also found some potential proxy variables. However, this analysis does not tell us if our model will be unfair. It has just highlighted issues that could lead to an unfair model. In the next sections, we will build a model and show that its predictions are unfair. In the end, we will relate back to this exploratory analysis. We will see how it can help explain what is causing the unfair predictions.
Modelling
We build our model using the code below. We are using the XGBClassfier function (line 2). We train the model using the features and target variable we defined earlier on in the proxy variable section. We then get the predictions (line 6) and add them to our df_fair dataset (line 7). In the end, this model had an accuracy of 85%. The precision was 73% and the recall was 60%. We now want to measure how fair these predictions are.
Before we move on, you could replace this model with your own if you wanted to. Or you could experiment with different model features. This is because all of the fairness measures we will use are model agnostic. This means they can be used with any model. They work by comparing the predictions to the original target variable. Ultimately, you will be able to apply these metrics across most applications.
Definitions of Fairness
We measure fairness by applying different definitions of fairness. Most of the definitions involve splitting the population into privileged and unprivileged groups. You then compare the groups using some metric (e.g accuracy, FPR, FNR). We will see that the best metrics show who has benefitted from the model.
Typically, a model’s prediction will either lead to a benefit or no benefit for a person. For example, a banking model could predict that a person will not default on a loan. This will lead to the benefit of receiving a loan. Another example of a benefit could be receiving a job offer. For our model, we will assume Y = 1 will lead to a benefit. That is if the model predicts that the person makes above $50K they will benefit in some way.
Accuracy
To start let’s discuss the accuracy and why it is not an ideal measure of fairness. We can base the accuracy calculation on the confusion matrix in Figure 4. This is a standard confusion matrix used to compare model predictions to the actual target variable. Here Y = 1 is a positive prediction and Y=0 is a negative prediction. We will also be referring back to this matrix when we calculate the other fairness metrics.

Looking at Figure 5, you can see how we use the confusion matrix to calculate accuracy. That is accuracy is the number of true negatives and true positives over the total number of observations. In other words, accuracy is the percentage of correct predictions.

Table 4 gives the accuracy of our model by the protected features. The ratio column gives the accuracy of the unprivileged (0) to privileged (1). For both protected features, you can see that the accuracy is actually higher for the unprivileged group. These results may mislead you to believe that the model is benefiting the unprivileged group.

The issue is that accuracy can hide the consequences of a model. For example, an incorrect positive prediction (FP) would decrease accuracy. However, the person would still benefit from this prediction. For example, even if the prediction is incorrect they would still receive a loan or a job offer.
Equal opportunity (true positive rate)
To better capture the benefits of a model we can use the true positive rate (TPR). You can see how we calculate TPR in Figure 6. The denominator is the number of actual positives. The numerator is the number of correctly predicted positives. In other words, TPR is the percentage of actual positives that were correctly predicted as positive.
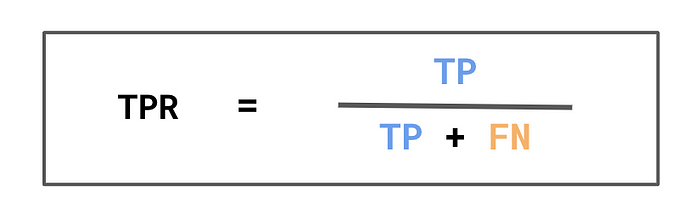
Remember, we are assuming a positive prediction will lead to some benefit. This means the denominator can be seen as the number of people who should benefit from the model. The numerator is the number who should and have benefited. So TPR can be interpreted as the percentage of people who have rightfully benefitted from the model.
For example, take a loan model where Y=1 indicates the customer did not default. The denominator would be the number of people who did not default. The numerator would be the number who did not default and we predicted them to not default. This means the TPR is the percentage of good customers we gave loans to. For a hiring model, it would be interpreted as the percentage of good quality candidates who received job offers.
Table 5 gives the TPRs of our model. Again, the ratio gives the TPR of the unprivileged (0) to privileged (1). In comparison to accuracy, you can see that the TPRs are lower for the unprivileged group. This suggests that a smaller percentage of the unprivileged group has rightfully benefitted from the model. That is a smaller percentage of high-income earners were correctly predicted as having a high income.

Like with prevalence, we can go further by finding the TPR at the intersection of the protected features. You can see these values in Table 6. Notice how the TPR is even lower when the person is in both unprivileged groups. In fact, the TPR for white males is over 50% higher than for non-white females.

Using the TPRs leads us to our first definition of fairness in Equation 1. Under equal opportunity we consider a model to be fair if the TPRs of the privileged and unprivileged groups are equal. In practice, we will give some leeway for statistic uncertainty. We can require the differences to be less than a certain cutoff (Equation 2). For our analysis, we have taken the ratio. In this case, we require the ratio to be larger than some cutoff (Equation 3). This ensures that the TPR for the unprivileged group is not significantly smaller than for the privileged group.

The question is what cutoff should we use? There is actually no good answer to that. It will depend on your industry and application. If your model has significant consequences, like for mortgage applications, you will need a stricter cutoff. The cutoff may even be defined by law. Either way, it is important to define the cutoffs before you measure fairness.
False negative rate
In some cases, you may want to capture the negative consequences of a model. You can do this using the FNR seen in Figure 8. Again, the denominator gives the number of actual positives. Except now we have the number of incorrectly predicted negatives as the numerator. In other words, the FNR is the percentage of actual positives incorrectly predicted as negative.

The FNR can be interpreted as the percentage of people who have wrongfully not benefitted from the model. For example, it would be the percentage of customers who should have but did not receive loans. For our model, it is the percentage of high-income earners who were predicted as having a low income.
You can see the FNR for our model in Table 7. Now the FNRs are higher for the unprivileged groups. In other words, a higher percentage of the privileged group have wrongfully not benefitted. In this sense, we have a similar conclusion to when using the TPRs with equalized odds. That is the model seems to be unfair towards the unprivileged groups.

In fact, requiring the FNRs to be equal would give us the same definition as equal opportunity. This is because of the linear relationship seen in Equation 1. In other words, equal TPRs would mean we also have equal FNRs. You should keep in mind that we would now require the ratio to be less than some cutoff (Equation 2).

It may seem unnecessary to define equal opportunity using FNRs. However, in some cases framing the definition using negative consequences can better drive your point home. For example, suppose we build a model to predict skin cancer. The FNR would give the percentage of people who had cancer but were not diagnosed with cancer. These errors could potentially be lethal. Ultimately, framing fairness in this way can better highlight the consequences of having an unfair model.
Equalized odds
Another way we can capture the benefits of a model is by looking at false positive rates (FPR). As seen in Figure 10, the denominator is the number of actual negatives. This means the FPR is the percentage of actual negatives incorrectly predicted as positive. This can be interpreted as the percentage of people who have wrongfully benefited from the model. For example, it would be the percentage of unqualified people who received a job offer.
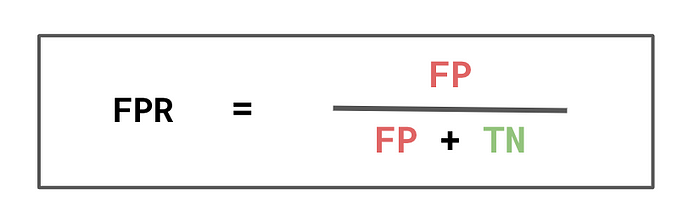
For our model, FPR would give the number of low-income earners predicted as having a high income. You can see these values in Table 8. Again we have higher rates for the privileged group. This tells us that a higher percentage of the privileged group has wrongfully benefited from the model.

This leads us to the second definition of fairness, equalized odds. Like with equal opportunity, this definition requires that the TPRs are equal. Now we also require that the FPRs are equal. This means equalized odds can be thought of as a stricter definition of fairness. It also makes sense that for a model to be fair overall benefit should be equal. That is a similar percentage of the groups should both rightfully and wrongfully benefit.

An advantage of equalized odds is that it does not matter how we define our target variable. Suppose instead we had Y = 0 leads to a benefit. In this case the interpretations of TPR and FPR swap. TPR now captures the wrongful benefit and FPR now captures the rightful benefit. Equalized odds already uses both of these rates so the interpretation remains the same. In comparison, the interpretation of equal opportunity changes as it only considers TPR.
Disparate impact
Our last definition of fairness is disparate impact (DI). We start by calculating the PPP rates seen in Figure 12. This is the percentage of people who have either been correctly (TP) or incorrectly (FP) predicted as positive. We can interpret this as the percentage of people who will benefit from the model.

For our model, it is the percentage of people who we predict to have a high income. You can see these values in Table 9. Again, these figures suggest that the model is unfair towards the unprivileged group. That is a smaller percentage of them are benefiting from the model. Although, when interpreting these values we should consider a drawback to this definition. We discuss this at the end of the section.

Under DI we consider a model to be fair if we have equal PPP rates ( Equation 1). Again, in practice, we use a cutoff to give some leeway. This definition is supposed to represent the legal concept of disparate impact. In the US there is a legal precedent to set the cutoff to 0.8. That is the PPP for the unprivileged group must not be less than 80% of that of the privileged group.

The issue with DI is that it does not take the ground truth into account. Think back to the prevalence values in the exploratory analysis. We saw that these were skewed. Where we had higher values for the privileged group. For a perfectly accurate model, we would have no false positives. This means the prevalence ratio would be the same as the disparate impact ratio. In other words, even for a perfectly accurate model, we may still have a low disparate impact ratio.
In some cases, it may make sense to expect equal prevalence or DI. For example, we would expect a model to predict an equal percentage of males and females to be high-quality candidates for a job. In other cases, it doesn’t make sense. For example, lighter skin is more susceptible to skin cancer. We would expect a higher prevalence of skin cancer in lighter skin. In this case, a low DI ratio is not an indication of an unfair model.
Fairness definition code
We use the function, fairness_metrics, to get all the results above. This takes a DataFrame with actual (y) and predicted target values (y_pred). It uses these to create a confusion matrix (line 5). This has the same 4 values that we saw in Figure 4. We get these 4 values (line 6) and use them to calculate the fairness metrics (lines 8–13). We then return these metrics as an array (line 15).
You can see how we use this function for the race protected feature below. We start by passing subgroups of the population to the fairness_metrics function. Specifically, we get the metrics for the privileged (line 2) and unprivileged (line 3) groups. We can then take the ratio of the unprivileged to privileged metrics (line 6).
Why is our model biased?
Based on the different definitions of fairness we have seen that our model is unfair towards the unprivileged groups. However, these definitions do not tell us why our model is unfair. To do that we need to do some further analysis. A good place to start is by going back to our initial exploratory analysis.
For example, using mutual information we saw that marital status was a potential proxy variable for sex. We can start to understand why this is by looking at the breakdown in Table 10. Remember, that marital-status = 1 indicates that the person is married. We can see that 62% of men are married. Whereas only 15% of the women in the population are married.

In Table 11, we can see that prevalence is over 6 times higher for those who are married. A model will use the relationship when making predictions. That is it is more likely to predict those who are married as earning over $50K. The issue is, as we have seen above, most of these married people will be males. In other words, females are less likely to be married and so the model is less likely to predict that they make above $50K.

In the end, there is still more work to do to fully explain why the model is unfair. When doing so we need to consider all the potential reasons for unfairness. We have touched on a few in this article. You can also read about them in-depth in the first article below. The next step is to correct unfairness. We look at both quantitative and non-quantitative approaches in the second article below.
I hope you found this article helpful! If you want to see more you can support me by becoming one of my referred members. You’ll get access to all the articles on medium and I’ll get part of your fee.
Image Sources
All images are my own or obtain from www.flaticon.com. In the case of the latter, I have a “Full license” as defined under their Premium Plan.
Dataset
Kohavi, R., and Barry Becker, B., (1996), Adult Data Set, Irvine, CA: University of California, School of Information and Computer Science (License: CC0: Public Domain) https://archive.ics.uci.edu/ml/datasets/adult
References
Pessach, D. and Shmueli, E., (2020), Algorithmic fairness. https://arxiv.org/abs/2001.09784
Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K. and Galstyan, A., (2021), A survey on bias and fairness in machine learning. https://arxiv.org/abs/1908.09635
Hardt, M., Price, E. and Srebro, N., 2016. Equality of opportunity in supervised learning. https://proceedings.neurips.cc/paper/2016/file/9d2682367c3935defcb1f9e247a97c0d-Paper.pdf
Besse, P., del Barrio, E., Gordaliza, P., Loubes, J.M. and Risser, L., 2021. A survey of bias in machine learning through the prism of statistical parity. https://arxiv.org/abs/2003.14263

